Позвонить: (4842) 75-75-05
Написать сообщение: m-40@inbox.ru

ЗАО «НПО «Механик» изготавливает цилиндрические шестерни с косым зубом со следующими характеристиками:
- Класс точности - до 6 включительно;
- Модуль - до 30 включительно;
- Диаметр - до 3 500 мм включительно.
Изготавливаем цилиндрические шестерни с косым зубом в штучном и серийном производстве. Возможно изготовление по образцам и эскизам заказчика. Индивидуальный подход.

Косозубые колёса являются усовершенствованным вариантом прямозубых. Их зубья располагаются под углом к оси вращения, а по форме образуют
часть спирали.
У косозубых колес оси зубьев располагаются не по образующей делительного цилиндра, а по винтовой линии, составляющей с образующей
угол β. С увеличением угла наклона линии зуба плавность зацепления и нагрузочная способность передачи увеличиваются,
но при этом увеличивается и осевая сила, что нежелательно. Поэтому угол наклона зубьев β принимают равным 8..18°,
он одинаков для обоих колес, но на одном из сопряженных колес зубья наклонены вправо, а на другом влево.
Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом. При работе такой передачи зубья входят в зацепление не
сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка распределяется на несколько зубьев.
В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность работы передачи и уменьшается шум.
Поэтому косозубые передачи имеют преимущественное распространение. В целом, косозубые колёса применяются в механизмах, требующих
передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.
Геометрия и кинематика косозубых цилиндрических передач
При работе косозубой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка
распределяется на несколько зубьев. В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность
работы передачи и уменьшается шум. Поэтому косозубые передачи имеют преимущественное распространение.
Основные геометрические размеры зависят от модуля и числа зубьев. При расчёте косозубых колёс учитывают два шага:
нормальный шаг зубьев pn - в нормальном сечении,
окружной шаг pt – в торцовом сечении; при этом pt=pn/cosβ.
Соответственно шагам имеем два модуля зубьев:
Окружной - mt=pt/π;
Нормальный - mp=pp/π
.
За расчётный принимают модуль mn, значение которого должно соответствовать стандартному. Это объясняется следующим:
для нарезания косых зубьев используется тот же инструмент, что и для прямозубых, но с соответствующим поворотом инструмента относительно
заготовки на угол. Поэтому профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба; следовательно, mn=m.
Диаметры делительный и начальный - d=dw=mt·z/cosβ
Диаметр вершин зубьев
da=d+2·mn
Диаметр впадин зубьев
df=d-2·mn
Межосевое расстояние
aw=(d1+d2)/2=mt(z1+z2)/2
Эквивалентное колесо
Профиль косого колеса в нормальном сечении соответствует исходному контуру инструментальной рейки и, следовательно, совпадает с профилем
прямозубого колеса.
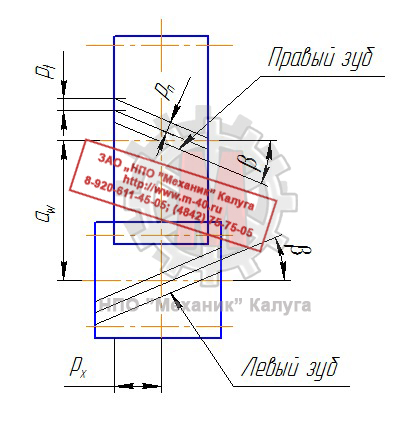
Рисунок 1. Геометрия косозубых цилиндрических передач
Расчет косозубых колес проводят через параметры эквивалентного прямозубого колеса. Нормальное к линии зуба сечение делительного цилиндра
имеет форму эллипса. Радиус кривизны эллипса при зацеплении зубьев в полюсе
rν=d/(2cosβ)
профиль зуба в этом сечении достаточно близко совпадает с
профилем приведённого прямозубого колеса, называемого эквивалентным,профиль зуба в этом сечении достаточно близко совпадает с профилем
приведённого прямозубого колеса, называемого эквивалентным.
Делительный диаметр - dν=2rν=d/(2cos2β)
Эквивалентное число зубьев - zν=dν/mn=d/(mncos2β)
или zν=dν/cos3β
где z – действительное число зубьев косозубого колеса. С увеличением β возрастает zν. Это одна из причин
повышения прочности косозубых передач.
По вопросам изготовления цилиндрических шестерен с косым зубом обращайтесь в отдел продаж по телефону:
(4842) 75-75-05
У косозубых колес оси зубьев располагаются не по образующей делительного цилиндра, а по винтовой линии, составляющей с образующей угол β. С увеличением угла наклона линии зуба плавность зацепления и нагрузочная способность передачи увеличиваются, но при этом увеличивается и осевая сила, что нежелательно. Поэтому угол наклона зубьев β принимают равным 8..18°, он одинаков для обоих колес, но на одном из сопряженных колес зубья наклонены вправо, а на другом влево.
Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом. При работе такой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка распределяется на несколько зубьев.
В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность работы передачи и уменьшается шум. Поэтому косозубые передачи имеют преимущественное распространение. В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.
Геометрия и кинематика косозубых цилиндрических передач
При работе косозубой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка
распределяется на несколько зубьев. В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность
работы передачи и уменьшается шум. Поэтому косозубые передачи имеют преимущественное распространение.
Основные геометрические размеры зависят от модуля и числа зубьев. При расчёте косозубых колёс учитывают два шага:
нормальный шаг зубьев pn - в нормальном сечении,
окружной шаг pt – в торцовом сечении; при этом pt=pn/cosβ.
Соответственно шагам имеем два модуля зубьев:
Окружной - mt=pt/π;
Нормальный - mp=pp/π
.
За расчётный принимают модуль mn, значение которого должно соответствовать стандартному. Это объясняется следующим:
для нарезания косых зубьев используется тот же инструмент, что и для прямозубых, но с соответствующим поворотом инструмента относительно
заготовки на угол. Поэтому профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба; следовательно, mn=m.
Диаметры делительный и начальный - d=dw=mt·z/cosβ
Диаметр вершин зубьев
da=d+2·mn
Диаметр впадин зубьев
df=d-2·mn
Межосевое расстояние
aw=(d1+d2)/2=mt(z1+z2)/2
Эквивалентное колесо
Профиль косого колеса в нормальном сечении соответствует исходному контуру инструментальной рейки и, следовательно, совпадает с профилем
прямозубого колеса.

Рисунок 1. Геометрия косозубых цилиндрических передач
Расчет косозубых колес проводят через параметры эквивалентного прямозубого колеса. Нормальное к линии зуба сечение делительного цилиндра
имеет форму эллипса. Радиус кривизны эллипса при зацеплении зубьев в полюсе
rν=d/(2cosβ)
профиль зуба в этом сечении достаточно близко совпадает с
профилем приведённого прямозубого колеса, называемого эквивалентным,профиль зуба в этом сечении достаточно близко совпадает с профилем
приведённого прямозубого колеса, называемого эквивалентным.
Делительный диаметр - dν=2rν=d/(2cos2β)
Эквивалентное число зубьев - zν=dν/mn=d/(mncos2β)
или zν=dν/cos3β
где z – действительное число зубьев косозубого колеса. С увеличением β возрастает zν. Это одна из причин
повышения прочности косозубых передач.
По вопросам изготовления цилиндрических шестерен с косым зубом обращайтесь в отдел продаж по телефону:
(4842) 75-75-05
Профиль косого колеса в нормальном сечении соответствует исходному контуру инструментальной рейки и, следовательно, совпадает с профилем прямозубого колеса.

Рисунок 1. Геометрия косозубых цилиндрических передач
Расчет косозубых колес проводят через параметры эквивалентного прямозубого колеса. Нормальное к линии зуба сечение делительного цилиндра
имеет форму эллипса. Радиус кривизны эллипса при зацеплении зубьев в полюсе
rν=d/(2cosβ)
профиль зуба в этом сечении достаточно близко совпадает с
профилем приведённого прямозубого колеса, называемого эквивалентным,профиль зуба в этом сечении достаточно близко совпадает с профилем
приведённого прямозубого колеса, называемого эквивалентным.
Делительный диаметр - dν=2rν=d/(2cos2β)
Эквивалентное число зубьев - zν=dν/mn=d/(mncos2β)
или zν=dν/cos3β
где z – действительное число зубьев косозубого колеса. С увеличением β возрастает zν. Это одна из причин
повышения прочности косозубых передач.
По вопросам изготовления цилиндрических шестерен с косым зубом обращайтесь в отдел продаж по телефону:
(4842) 75-75-05
| Январь 2025 | ||||||
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 | ||
| Муфты зубчатые в наличии | ||
| Муфты МЗ | ||
| Тип | Цена, руб., с НДС |
Кол-во, шт. |
| МЗ-1 | 9 850 | 26 |
| МЗ-2 | 15 300 | 180 |
| МЗ-3 | 17 200 | 2 |
| МЗ-4 | 26 200 | 21 |
| МЗ-5 | 33 600 | 12 |
| МЗ-6 | 56 500 | 12 |
| МЗ-7 | 78 200 | 0 |
| МЗ-8 | 105 600 | 7 |
| МЗ-9 | 133 000 | 10 |
| МЗ-10 | 185 000 | 4 |




